Пифагоровы штаны и другие геометрические секреты, о которых не рассказывали в школе

Сила из песков Египта

Египетские пирамиды. Грандиозные, загадочные, они до сих пор будоражат умы учёных. Как без современных компьютеров и лазерных нивелиров добиться такой ошеломительной точности? Оказывается, секрет иногда был предельно прост.

Представьте обычную верёвку с двенадцатью узелками, завязанными на равных промежутках. Всё. С её помощью египтяне получали идеально прямой угол. Как? Они складывали из этой верёвки треугольник со сторонами в 3, 4 и 5 частей. Такой треугольник всегда оказывается прямоугольным. Просто, гениально и задолго до того, как Пифагор сформулировал свою знаменитую теорему. Вот вам и «примитивные» древние цивилизации!

Как тень помогла измерить Землю

А теперь перенесёмся в III век до нашей эры, в Древнюю Грецию. Учёный по имени Эратосфен из Килены задался, казалось бы, неразрешимой задачей: узнать размер нашей планеты. И у него не было спутников. Зато было Солнце и острая наблюдательность.

Он знал, что в день летнего солнцестояния в городе Сиена (нынешний Асуан) солнце стоит в зените, и предметы не отбрасывают тени. В это же время в Александрии, что севернее, вертикальный шест отбрасывал вполне заметную тень. Эратосфен измерил угол, под которым падали солнечные лучи в Александрии. Он составил примерно 7,2 градуса — это ровно 1/50 часть полной окружности в 360 градусов.

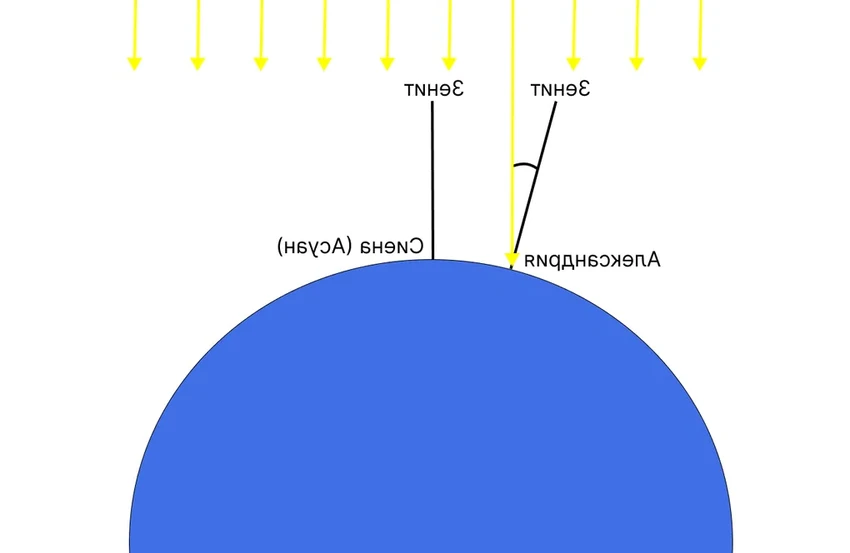
Оставалось узнать расстояние между городами (около 800 км по нашим меркам) и умножить его на 50. Получилось около 40 000 километров — окружность Земли! Точность для той эпохи просто поразительная. Не правда ли, красивое решение?

Геометрия на поле боя: правило большого пальца

А вот история, где геометрия была не просто любопытной наукой, а средством выживания. Во время Великой Отечественной войны солдаты использовали простейшее правило подобия треугольников для определения расстояния до цели.

Солдат вытягивал руку вперёд, поднимал большой палец и целился им в объект, скажем, в дерево или танк, стараясь полностью его закрыть. Длина пальца примерно 7 см, длина вытянутой руки — около 70 см. Получается прямоугольный треугольник, где один катет в 10 раз больше другого.

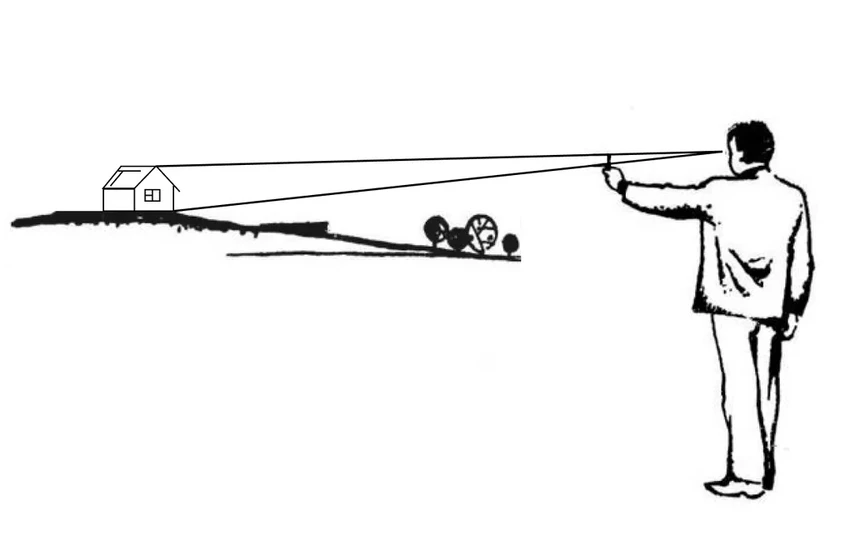
Если закрытый пальцем танк имеет известную высоту (например, 3 метра), то расстояние до него будет в те же 10 раз больше — то есть 300 метров. Конечно, позже появились специальные приборы, но их принцип работы был тем же самым. Геометрия в прямом смысле спасала жизни. Звучит как сюжет для фильма, да?

Про Пифагоровы штаны, которые на все стороны равны

Помните эту забавную фразу из школьного фольклора? «Пифагоровы штаны во все стороны равны». Она, конечно, не совсем точна с математической точки зрения, но зато невероятно наглядна!

Сама теорема Пифагора говорит, что квадрат гипотенузы равен сумме квадратов катетов. А если построить на сторонах прямоугольного треугольника три квадрата, то два поменьше (на катетах) по площади в сумме будут равны большому квадрату на гипотенузе. Если перевернуть эту конструкцию, то она действительно напоминает штаны с двумя расходящимися штанинами и одной общей «ширинкой». Гениальная мнемоника, которая помогла запомнить теорему миллионам школьников.

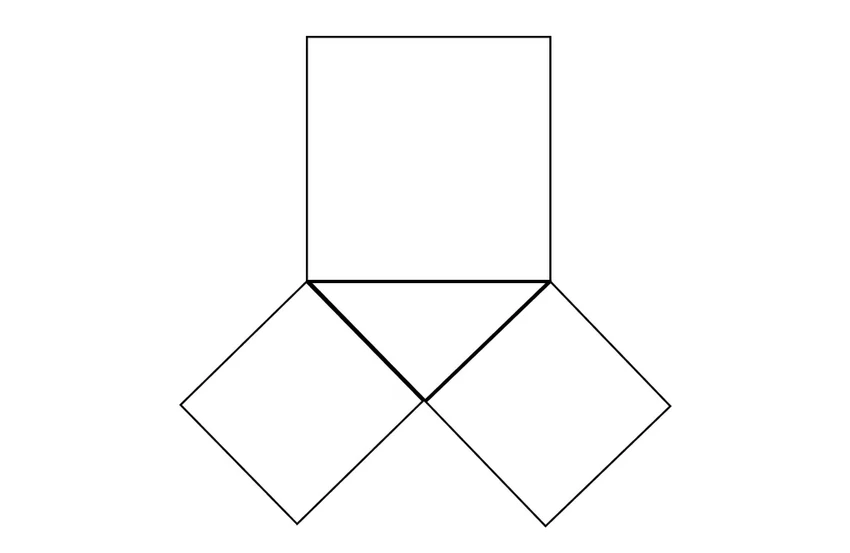
Пифагор, думаю, был бы в замешательстве от такого сравнения, но, возможно, и одобрил бы — главное, чтобы суть запомнили.

Божественная пропорция: почему нам нравится красивое

Есть в геометрии число, которое преследует человечество всю его историю — золотое сечение, примерно 1,618. Его обозначают греческой буквой φ (фи). Это такое деление целого на две части, при котором отношение большей части к меньшей равно отношению всего целого к большей части. Звучит сложно, но выглядит невероятно гармонично.

Древние греки, от Пифагора до Евклида, обожали исследовать это отношение. Они чувствовали его гармонию интуитивно. Взгляните на Парфенон в Афинах — его пропорции подчиняются золотому сечению. Не потому, что у архитекторов был калькулятор, а потому, что такое соотношение воспринимается нами как идеально сбалансированное, совершенное.

Эта «божественная пропорция» встречается в природе, искусстве и архитектуре по сей день. Художники и дизайнеры часто неосознанно используют соотношения, близкие к 3/8 и 5/8. Выходит, геометрия — это не только про вычисления, но и про саму суть красоты. Интересно, правда?