AlphaGeometry: геометрические доказательства на уровне олимпийского золота

Команда Google DeepMind создала инструмент, который умеет доказывать геометрические теоремы — те самые про треугольники и окружности — с такой же строгостью, как и участники Международной математической олимпиады. Название у этого цифрового «вундеркинда» соответствующее — AlphaGeometry.

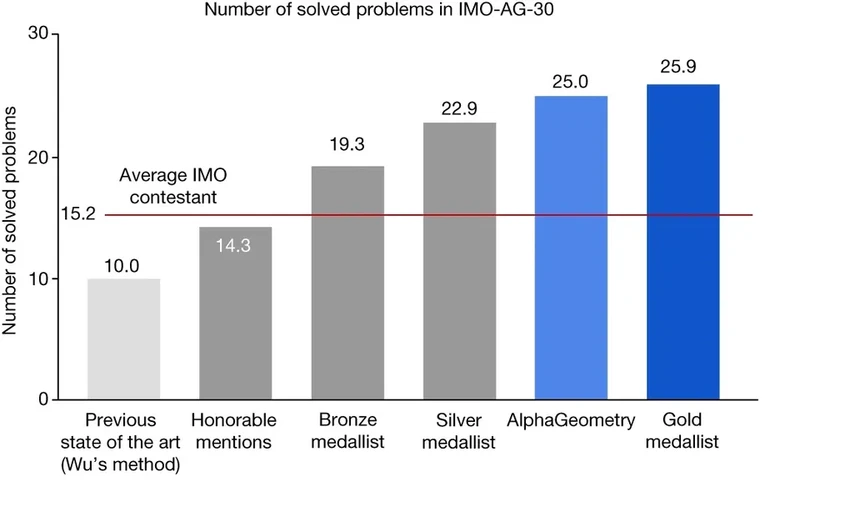
Её протестировали на 30 каверзных задачах из прошлых олимпиад. Результат? 25 решенных. Это уровень, близкий к золотым медалистам, по крайней мере, в разделе геометрии. Неплохо для «железного» студента, согласитесь?

Правда, Кевин Баззард, математик из Имперского колледжа Лондона, справедливо замечает, что геометрия — лишь одна из многих дисциплин на олимпиаде. Компьютеру может быть куда сложнее взять верх, скажем, в теории чисел. Тем не менее, он признает: «То, что им удалось решить 25 олимпиадных задач и выдать при этом понятные человеку доказательства, само по себе впечатляет».

Давайте посмотрим, как AlphaGeometry выглядит на фоне живых соперников.

Языковой барьер, или Почему бот-математик не болтает попусту

Вы наверняка слышали про чат-ботов вроде ChatGPT, которые генерируют тексты на любую тему. Ученые пробовали заставить подобные языковые модели решать математические задачи. Получалось интересно, но... часто бессмысленно. Бот мог дать верный числовой ответ, а вот его текстовое объяснение оказывалось полной ерундой, которую приходилось перепроверять вручную.

«Если система обучена на обычном языке, она и строить вывод будет на обычном языке, которому мы не можем слепо доверять», — поясняет Триу Трин из Google DeepMind, один из авторов работы. И тут возникает резонный вопрос: а зачем тогда этот посредник?

Вместо этого команда создала специальный язык для доказательств с жестким синтаксисом, похожим на язык программирования. Его ответы легко проверяются компьютером, но при этом остаются понятными и для человека. В этот язык зашили десятки базовых геометрических правил (вроде «через две точки можно провести прямую»), а затем сгенерировали на нём 100 миллионов синтетических «доказательств» — случайных, но логически безупречных цепочек шагов.

AlphaGeometry училась на этих искусственных данных. Она решала задачи, выстраивая шаг за шагом, подобно тому как чат-бот генерирует текст. Но благодаря тому, что её вывод был машиночитаемым, любую ошибку можно было сразу отловить. Перебирая множество вариантов и автоматически отсеивая неверные, система в итоге выдавала корректное решение даже для олимпиадных головоломок.

Сила в гибриде: когда интуиция встречает логику

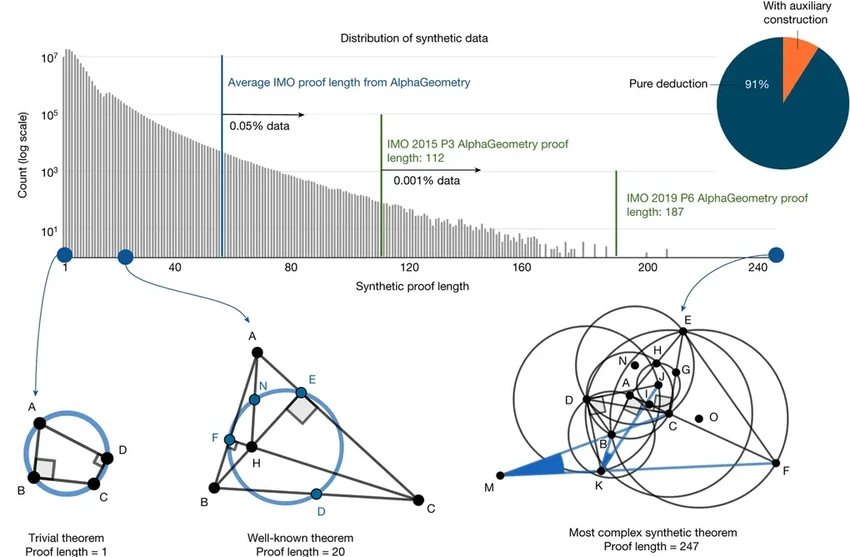
В чём секрет AlphaGeometry? В удачном браке двух подходов: статистических догадок языковой модели (что-то вроде интеллектуального перебора) и строгих символических рассуждений. Как отмечает Стефан Шульц из университета Баден-Вюртемберга, именно сочетание этих столь разных методов может быть источником её силы.

Обучение на синтетических данных устраняет ещё одну серьёзную проблему. Когда нейросеть учится на текстах из интернета, нельзя гарантировать, что она раньше не видела готовое решение. Здесь же она каждый раз вынуждена находить доказательство самостоятельно. Как подчеркивает соавтор исследования Хе Хе из Нью-Йоркского университета, цель как раз и состояла в том, чтобы построить систему без человеческих данных, которая однажды сможет превзойти человеческие возможности.

Означает ли это, что математики останутся без работы? Вряд ли. «Можно представить, что через несколько лет подобные методы смогут решать задачи уровня самых талантливых студентов», — рассуждает Баззард. — «Но я не вижу никаких свидетельств, что машины способны автономно работать на переднем крае современной математики». И в этом, наверное, есть наше временное утешение.