Физики построили невероятный лабиринт, превосходящий по сложности древний миф о Дедале

Работа команды Фликера, подробно описанная в журнале Physical Review X, — это пример того, как абстрактная математика встречается с физикой материалов.

Квазипериодические мозаики

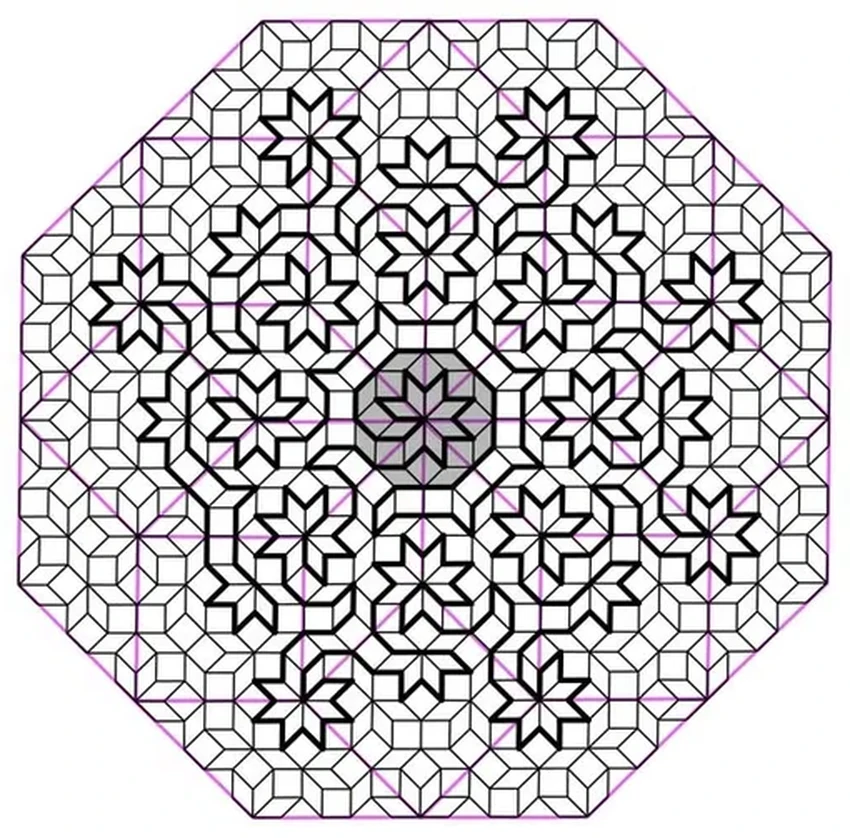
Всё началось с мозаики Аммана-Бинкера. Её главная фишка — она покрывает плоскость, но не периодически. Поясню. Возьмём обычную плитку-квадрат: кладём ряд, сдвигаем — и узор повторяется. Это трансляционная симметрия. Таких замощений много.

А вот нобелевский лауреат Роджер Пенроуз когда-то задался каверзным вопросом: а можно ли замостить плоскость так, чтобы узор НИКОГДА не повторялся? Оказалось, можно! Его знаменитые мозаики Пенроуза и есть такие квазипериодические структуры. Сдвиньте фрагмент — и точного совпадения вы не найдёте. Будет похоже, но не то. Мозаика Аммана-Бинкера из той же семьи.

Физики решили поискать на этой мозаике цикл Гамильтона — такой элегантный маршрут, который проходит через каждую вершину ровно один раз, возвращается в начало и нигде сам себя не пересекает. Разумеется, не для бесконечной плоскости, а для её большого фрагмента. Задача адски сложная. Но учёных осенила идея из... шахмат!

Знаете задачу обходе доски конём? Нужно побывать на всех клетках один раз и вернуться. Этот маршрут коня — и есть цикл Гамильтона для шахматной доски. Физики попробовали применить ту же логику «хода коня» к вершинам мозаики. И у них получилось! Найденный путь они и назвали самым сложным лабиринтом в мире. И неспроста — попробуйте пройти его мысленно.

Квазикристаллы

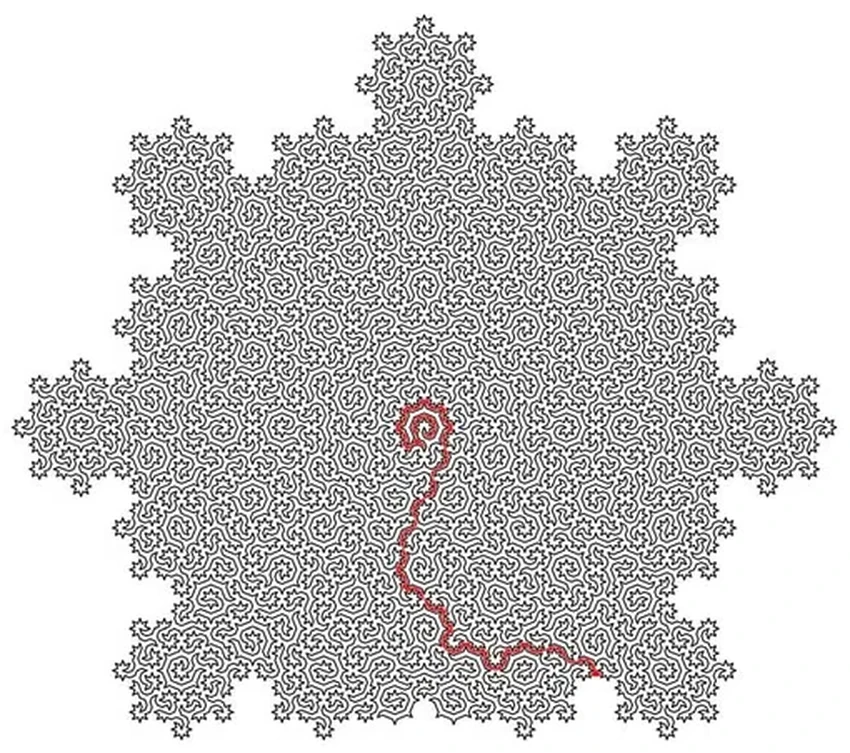
А где же здесь кристаллы? В том-то и дело. Квазикристаллы — это редчайшая в природе форма материи, нечто среднее между идеальным порядком и хаосом.

В обычном кристалле (соль, алмаз) атомы выстроены в строгую трёхмерную решётку с повторяющимся узором. Сдвинул фрагмент — он совпал. В аморфном теле (как стекло) — атомы расположены почти хаотично.

А вот квазикристалл — это материал с упорядоченным, но не повторяющимся узором, как мозаика Пенроуза. Трансляционной симметрии нет, но есть «дальний порядок»: смотришь издалека — кажется правильным, а вблизи — бесконечно сложный, неповторяющийся узор.

Используя мозаики Аммана-Бинкера как модель, физики получили те самые гамильтоновы циклы, которые, по их мнению, описывают атомную структуру квазикристалла. Представьте нить, которая соединяет все атомы в образце, касаясь каждого лишь раз и никогда не пересекаясь. Элегантно, не правда ли?

Находить такие циклы невероятно трудно. Новый подход потенциально способен пролить свет на кучу других сложнейших задач — от оптимизации маршрутов до фолдинга белков.

Есть и практический выход. Квазикристаллы — отличные кандидаты для захвата углерода или хранения водорода (помните водородные двигатели?). Молекулы газов можно аккуратно размещать как раз вдоль этих проложенных «гамильтоновых дорожек».

Но главная ценность работы, пожалуй, не в приложениях. Она — в красивом слиянии идей. Шахматы, древние лабиринты, непериодические замощения и физика конденсированного состояния... Когда такие разные миры проникают друг в друга, рождается по-настоящему новое знание. Разве не ради этого мы и занимаемся наукой?